Primitive Pythagorean Triples

Pythagorean Triples are positive integer solutions (a, b, c) to the equation a² + b² = c². Primitive Pythagorean Triples are those for which a, b, and c are relatively prime (have no common divisor greater than 1).

The Euclidean Algorithm

Suppose a and b are both positive integers. Then the greatest common divisor (gcd) of a and b is defined as the largest positive integer d that divides both a and b:

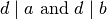
where means “divides”.

The Euclidean Algorithm was invented over 2000 years ago to find the greatest common divisor of two numbers. The algorithm is based on the following insight:

Take two positive integers, a and b. Assume a ≤ b. Then, a and b, and a - b and b, have the same set of common divisors. In particular, gcd(a, b) = gcd(a - b, b).

This is useful because the numbers on the right-hand side are smaller (at least, one of them is), than the numbers on the left-hand side. This idea can be applied over and over again, to reduce the size of the problem by working with successively smaller numbers. The algorithm can be expressed as follows:

1. Start with two numbers a and b.
2. Subtract the smallest from the largest.
3. Repeat until the numbers are the same.
4. This last number is gcd(a, b).

Report Description

The report consists of the following exercises. Once you have the exercises complete, write a report containing your results and conclusions. Refer to the “Grading” web page or the class notes for the structure of the reports and what they should contain.

Exercise 1. Greatest Common Divisor

• Write a function mygcd(a, b) that implements the Euclidean algorithm to return the greatest common divisor of two positive integers a and b.
• Test this function to make sure that it is working correctly.

Exercise 2. Perfect Squares

• Write a function is_square(x) that returns True if x is a perfect square and False otherwise.
• Test this function to make sure that it is working correctly.

Exercise 3. Generate Primitive Pythagorean Triples

• Generate all Primitive Pythagorean Triples for a, b ≤ 5000 (just generate them - you don’t need to print them all out.)
• State how many PPTs you have found.

Exercise 4. Plot and Analyze Your Results

• See if there is any discernible structure in the Primitive Pythagorean Triples.

Hints and Suggestions for the Report

Writing the mygcd and is_square Functions

• It’s a good idea to use print functions inside your functions to check that code is working as expected. For example, printing out a and b inside the while loop in your mygcd function will show the algorithm working step-by-step. These statements can be commented out later using #.

Generating the Primitive Pythagorean Triples

• Use mygcd(a, b) == 1 to check if a and b are relatively prime.
• Use is_square(a**2 + b**2) to test if a² + b² is a perfect square.
• Test your code using small numbers first, maybe a, b ≤ 100. Make sure the code is working on these small numbers before moving on to bigger numbers.

Plotting and Analyzing the Results

• Generate graphs using Matplotlib plot to look for patterns.

  • At a minimum, plot the points (a, b) for the PPTs you have found.
  • If you can, find a way to filter the (a, b) pairs to remove the duplicate (b, a) pairs.
  • Feel free to plot other graphs that might show other kinds of structure.

• Look at the Primitive Pythagorean Triples as well by printing some out.

  • Include the value of c as well as (a, b) when printing the PPTs. You may want to convert c to an integer before printing it.
  • Are there any kinds of mathematical regularity that you can see?
  • Can you find reasons for any of these regularities?