Syllabus

Course Description

This course provides a broad introduction to computing in the sciences and in both abstract and applied mathematics. It is accessible to students early in their undergraduate program, thereby opening the door to the profitable use of computation throughout the junior and senior years.

The course covers the following areas:

• Programming using Python, the scientific computing package NumPy, and the plotting library Matplotlib.
• Applications of scientific computing in number theory, linear regression, dynamical systems, initial value problems, random number generation and optimization.
• Using computers to explore topics in the mathematical and natural sciences.
• Presentation of experiments, observations and conclusions in the form of written reports.

Prerequisities: MTH 141 and MTH 142 or MTH 154. No prior programming experience is needed.

Course Materials

Textbook: There is no required textbook for this class. We will be using online resources and extensive class notes. If you would like a book for reference, then either “Scientific Computation” by Bruce E. Shapiro (Sherwood Forest Books, 2015) or “Python for Scientists” by John M. Stewart (Cambridge University Press, 2014) is recommended.

Python: We will be using Python 3.5. It is strongly recommended that you use the Anaconda distribution, which is available free on Windows, Mac and Linux and contains all the packages we need (NumPy, SciPy, Jupyter, Matplotlib).

Jupyter Notebook: Reports will be written in Jupyter Notebook. This is included as part of the Anaconda distribution.

UBlearns: The course page on UBlearns will be used for submitting assignments and posting grades.

Website: http://www.acsu.buffalo.edu/~adamcunn/spring2017/MTH337.html

Course Requirements

Laptop/Tablet: Classes take place in the Math Building and involve programming, so expect to bring your laptop/tablet to every class.

Class participation: Aspects include attending class, asking and answering questions in class and Piazza, and involvement in any group activities.

Quizzes: Short quizzes will be held weekly in class.

Reports: Reports will be submitted every two weeks via UBLearns. The submission deadline will usually be 9am on a Tuesday. You are free to discuss the homework with others, but the work you turn in should be written by you alone.

Report Portfolio: You will generate a final portfolio combining all your reports into a single document.

Grading Policy

Course Grades will be determined with the weightings:

Weekly reports and final portfolio	70%
Quizzes	20%
Participation	10%

4-point Grading Scale: Reports will be assigned a letter grade on a four point grading scale:

A+ = 4.33	A = 4.00	A- = 3.67
B+ = 3.33	B = 3.00	B- = 2.67
C+ = 2.33	C = 2.00	C- = 1.67
D+ = 1.33	D = 1.00	D- = 0.67

+/- grades will be used in the computation of your overall grade. Note that the university does not permit A+ or D- grades.

Lowest Report Dropped: The lowest report grade will be dropped when computing your overall grade.

Extra Credit: Up to one full grade of extra credit (e.g. B 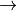A) is available on every report for extra or unusual work or insight.

Late Assignment Policy: Reports are usually due by 9am on a Tuesday. Late reports will be accepted up to three days late, with a penalty of one full grade (e.g. A 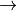B) for each day late.

Incompletes: Incompletes will be given only under extraordinary circumstances (such as surgery during the last week of class).

Expectations for this class

Attendance: You are expected to attend every class. If you miss a class you are responsible for getting the homework, lecture notes and any other in-class information or materials from a classmate.

Independent research: We cannot cover every single option available in Python in the limited time we have in class. It is expected therefore that you make use of the online resources to do research for youself. If there is something that you want to do, the chances are that Python already has a way to do it - you just need to find it.

Absolutely no non-class-related computer or phone use during class: (e.g. texting, Facebook, emailing): the penalty will be one third of a letter grade off overall course grade for each instance.

Academic Honesty: Students are expected to adhere to the university policy on academic honesty. Note particularly that

Written works must be the complete and original effort of the student, with all ideas and words of others duly attributed.

Cheating, plagiarism, or misrepresentation of your work will result in formal charges.

How to succeed: Sustained steady effort, starting from day one. Make full use of the resources available to you: the classnotes, website, online documentation, Piazza, and each other. See me in office hours, email me, or make an appointment to see me at some other time. Start homework assignments early - programming and debugging often take more time than anticipated.

Other

Important dates:

Mon Feb 6 – Last day to drop the course - no record appears on transcript.

Fri Apr 21 – Last day to resign from the course - an “R” appears on the transcript.

Students with Disabilities: If you have a diagnosed disability (physical, learning or psychological) which will make it difficult for you to carry out the course work as outlined, or requires accommodations such as recruiting note takers, readers or extended time on quizzes and/or assignments, please advise me during the first two weeks of the course so that we may review possible arrangements for reasonable accommodations.

Student Learning Outcomes

Assessment measures: bi-weekly programming assignments, in-class quizzes.

At the end of this course, students will be able to:	Assessment
use Jupyter Notebooks to write computer programs in the Python language. use Markdown to format text within Jupyter Notebooks. use LaTex to format mathematical expressions within Jupyter Notebooks.	All reports
communicate their work in formal research-style reports.	All reports
define and use Python integer, float, complex and boolean data types. define and use Python list, string, tuple, set and dictionary data structures. understand and use Python list comprehensions and generators.	All reports
use the Python print and format commands to format and display results.	All reports
use the Python control constructs if, else and elif. use Python for and while loops, and break and continue statements. define functions in Python using positional and keyword arguments.	All reports
display numerical data using several Matplotlib plotting commands. fully and accurately label Matplotlib graphs. display multiple plots using the Matplotlib subplot command.	All reports
use NumPy array creation operations. understand the concepts of vectorization and array operations. access NumPy arrays using indexing and slicing. use NumPy boolean and integer array indexing.	Reports 2 - 7
time the execution of code using the IPython %timeit and%%timeit magics.	Reports 3 - 7
understand how the RGB color model can be used to represent colors. create color images using NumPy multidimensional arrays. load, save and display images using imread, imsave and imshow.	Report 4
generate animations using the Matplotlib animation library.	Report 5
load and write text data to and from files.	Report 7
understand and implement Euclid’s algorithm for the greatest common divisor. test conjectures in number theory by finding examples or counterexamples. search for patterns in the integers by making appropriate graphics.	Report 1
understand the principles and details of the IEEE 754 floating point standard. recognize the pitfalls of using floating-point arithmetic. use algebraic reformulation and Taylor-series approximations to avoid these pitfalls.	Report 2
understand the notion of a discrete dynamical system. explore the dynamics of such systems, including simple models of population dynamics. understand the distinction between transient and asymptotic behavior. understand the concept of non-periodic asymptotic behavior. use color to make visual representations of the dynamics.	Report 3
find the “best-fit” to a data set using least squares linear regression.	Report 3
Solve a nonlinear equation in a single variable by bisection and by Newton’s method. Understand the concepts of linear, quadratic and superlinear convergence. Understand some stopping criteria for root-finding methods.	Report 4
understand the arithmetic of the complex numbers. explore the dynamics of discrete dynamical systems in the complex plane. use color to make visual representations of the dynamics.	Report 4
understand the concept of a system of ordinary differential equations. solve systems of ODEs using Euler’s and Heun’s methods, and display the solutions. formulate and solve the equations of motion of a planet orbiting a binary star.	Report 5
understand the need for random numbers to model physical and social systems. use a linear congruential generator to generate uniform pseudo-random numbers. understand and verify through simulation the Central Limit Theorem. generate non-uniform random numbers with a specified distribution. apply Monte-Carlo methods to estimating areas inside curves. understand and simulate a model of surname extinction using Monte-Carlo methods.	Report 6
write computer programs to manipulate and analyze text. implement an n-gram statistical language model using word frequencies in online texts.	Report 7
use Python to access bioinformatics databases and identify nucleotide base sequences.	Report 7

The table below indicates to what extent this course reflects each of the learning objectives of the undergraduate mathematics program. A description of learning objectives is available online.

Skill:	Computational	Analytical	Problem Solving	Research	Communication
Present:	extensively	moderately	extensively	moderately	extensively

Class Schedule

Week	Programming Topics	Mathematical Topics
1	Introduction to Jupyter Notebook Numbers, variables, loops, functions	The Euclidean Algorithm
2	Lists, namespaces Matplotlib basic plotting	Pythagorean Triples
Report 1: Primitive Pythagorean Triples, due 2/14
3	Break, continue, list comprehensions NumPy arrays and vectorization	Binary numbers Floating point numbers
4	NumPy array indexing and slicing	Floating-point arithmetic Hazards of floating-point arithmetic
Report 2: Floating Point Numbers, due 2/28
5	NumPy multidimensional arrays Timing code execution	Deterministic dynamical systems The logistic population model
6	Matplotlib logarithmic plots Matplotlib subplots	The “butterfly effect” Linear least squares
Report 3: The Mayfly Model and the Butterfly Effect, due 3/14
7	RGB color representation Image creation and display	Root-finding methods Convergence of root-finding methods
Spring break
8	NumPy fancy indexing	Complex arithmetic
Report 4: Newton in the Complex Plane, due 4/4
9		Continuous dynamical systems Initial value problems
10	Matplotlib animations	Solving differential equations
Report 5: Tatooine, due 4/18
11	Matplotlib histograms Matplotlib polar plots	Random number generators Monte Carlo integration
12	NumPy random number generation NumPy axis-dependent operations	The Central Limit Theorem Non-uniform random numbers
Report 6: Random Numbers, due 5/2
13	Python dictionaries String manipulation functions	Conditional probabilities Maximum likelihood estimates
14	Matplotlib pie charts
Report 7: Statistical Language Models, due 5/13
Report Compilation, due 5/21