Statistical Language Models¶
A statistical language model assigns a probability P(S) to a sentence of n words, S = w1 w2 ... wn. The chain rule in probability theory describes how to factor P(w1, w2, ..., wn) into the probabilities of each word given the words that precede it.
P(S) = P(w1) P(w2 | w1) P(w3 | w1 w2)P(wn | w1, w2, ..., wn - 1)
We use here the notation P(B | A). If we know that an event A has occurred, then the probability of an event B given that A has already occurred is called the conditional probability of B given A, denoted P(B | A).
N-Gram Models¶
In practice, most possible word sequences are never observed even in a very large corpus (a body of text). One solution when constructing a language model is to make the Markov assumption that the probability of a word depends only on the most recent words that preceded it. An n-gram model does just this, and predicts the probability of a word based only on the n - 1 words before it.
For n = 1, 2 and 3 we have:
- Unigram: P(wi | w1, w2, ..., wi - 1) ≈ P(wi)
- Bigram: P(wi | w1, w2, ..., wi - 1) ≈ P(wi | wi - 1)
- Trigram: P(wi | w1, w2, ..., wi - 1) ≈ P(wi | wi - 1, wi - 2)
The simplest way to estimate these probabilities is to compute the maximum likelihood estimate from the number of times a word sequence occurs in the corpus used to train the model. If we let C(w1, w2, ...) denote the number of times the sequence w1, w2, ... is seen in the corpus, then we have:
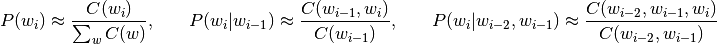
Evaluating Models: Perplexity¶
The performance of an n-gram model is often evaluated using a metric called perplexity. This measures how well the model predicts a text W = w1 w2 ... wN of length N using the formula:
![PP(W) = \sqrt[N]{\dfrac{1}{P(w_1 w_2 \ldots w_n)}}](_images/math/e2b3cf94a8bd38f0ea3458b61492426fa820d4d1.png)
Expressing P(W) as the product of conditional probabilities, this becomes:
![PP(W) = \sqrt[N]{\prod_{i=1}^N \dfrac{1}{P(w_i | w_1, \ldots, w_{i-1})}}](_images/math/d1b38caba4db57e46e1d9aa82c1a3e33f0f2ad99.png)
A useful way to think about perplexity is as the average number of possible next words that can follow any word. This is also known as the branching factor. For example, if each word in a language was always followed by five others with equal probability, then the perplexity would be:
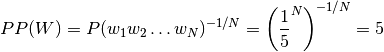
Report Description¶
In this report we download texts from online sources, analyze the distribution of words in these texts, and use them to generate statistical language models of increasing levels of complexity. The report consists of the following exercises:
Exercise 1. Word Frequency Analysis
- Download the text of Shakespeare’s “Hamlet” from Project Gutenberg.
- Make a list of all the words in this text, ordered by frequency.
- Identify the most commonly used words.
- Make a pie chart of the words, showing their frequency.
- Plot the frequency of words against their rank in frequency order and comment on any patterns.
- Perform the word frequency analysis on another text of your choice and comment on any differences.
Important
Please do not print out the complete text of “Hamlet” (or any other text) in the report you submit! Similarly, please don’t print out any of the models. These make the document unnecessarily long, difficult to load and read, and serve no purpose.
Exercise 2. N-Gram Models
- Select an author of your choice and download either their collected works or as many individual works as possible from Project Gutenberg.
- Construct unigram, bigram, trigram and quadrigram models from this corpus.
- Print the number of distinct words, bigrams, trigrams and quadrigrams found in this corpus.
Exercise 3. Generate “Random” Sentences
- Generate at least a paragraph of “random” sentences using each model created in Exercise 2.
- How large does ‘N’ need to be before these sentences seem gramatically correct?
- How large do you think ‘N’ needs to be before your chosen author could be identified from these sentences?
Exercise 4. Perplexity
- Use the definition of perplexity given above to calculate the perplexity of the unigram, bigram, trigram and quadrigram models on the corpus used for Exercise 2.
- Make some observations on your results.
Important
Because the probability of any long text is extremely low, calculating the perplexity directly will lead to an underflow error. Calculate instead the logarithm of the perplexity, then convert back.
![\log(PP(W)) &= \log\left(\sqrt[N]{\prod_{i=1}^N \dfrac{1}{P(w_i | w_1, \ldots, w_{i-1})}}\right) \\
&= -\dfrac{1}{N} \sum_{i=1}^N \log (P(w_i | w_1, \ldots, w_{i-1}))](_images/math/84de8c2d6430042f61cb73cca962c556103a23ad.png)
The terms P(wi  w1, ..., wi - 1) are given by the conditional probabilities of the n-gram model. These will be calculated for each word in the text and plugged into the formula above.
w1, ..., wi - 1) are given by the conditional probabilities of the n-gram model. These will be calculated for each word in the text and plugged into the formula above.
Hints and Suggestions for the Report¶
Combining Multiple Text Files¶
Strings can be concatenated simply using ‘+’. For example:
mytext = "MTH" + "337"
If you download multiple files from Project Gutenberg, you can use this to create a single string that contains all the texts before you start generating the models.
Generating the N-Gram Models¶
The unigram model consists of one list of words and another list of their associated probabilities. All other models are stored as dictionaries.
- For the bigram model, the dictionary keys are single words.
- For the trigram model, the dictionary keys are (word1, word2) tuples.
- For the quadrigram model, the dictionary keys are (word1, word2, word3) tuples.
The dictionary values associated with these keys are the lists of possible following words and their conditional probabilities.
Generating the Random Sentences¶
Each word in a random sentence is generated by passing a list of words and their associated probabilities to numpy.random.choice.