Primitive Pythagorean Triples¶

Pythagorean triples are positive integer solutions 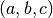$(a, b, c)$ to the equation 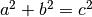$a^2 + b^2 = c^2$ . Primitive Pythagorean Triples are those for which 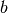$a$ , $b$ , and $c$ are relatively prime (have no common divisor greater than 1).

Report Description¶

Do the following exercises first to write the functions needed for the rest of the report:

Exercise 1. Write a function mygcd(a, b) that returns the greatest common divisor of two integers a and b.

Exercise 2. Write a function is_square(x) that returns True if 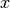$x$ is a perfect square and False otherwise.

Once you have these functions tested and working:

Generate all Primitive Pythagorean Triples for 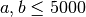$a, b \leq 5000$ (Just generate them - you don’t need to print them all out.)
See if there is any discernible structure in the PPTs.
Write a report containing your results and conclusions.

Hint

Use mygcd(a, b) == 1 to check if a and b are relatively prime.
Use is_square() to test if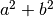 $a^2 + b^2$ is a perfect square.
Generate graphs using Matplotlib plot to look for patterns.

Note

Look at the Primitive Pythagorean Triples as well by printing some out. Are there any kinds of mathematical regularity that you can see? Can you find reasons for any of these regularities?

Tip

Test for small numbers first, maybe 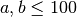$a, b \leq 100$ . Make sure the code is working on these small numbers first before moving on to bigger numbers.
It’s a good idea to use print statements inside your functions to check that code is working as expected. For example, printing out a and b inside the while loop in your mygcd function will show the algorithm working step-by-step. These statements can be commented out later using #.
Test the mygcd and is_square functions on their own first before generating the Primitive Pythagorean Triples.