This project looks into rather unique property of biometric matchers, matcher independence, and whether this property can be effectively utilized in their combination. Note, that independence assumption was sometimes previously applied in the combination of non-independent classifiers or features (Naive Bayesian), resulting in non-optimal combination. In this project we assume that we already have optimal combination algorithm, and want to investigate whether additional usage of independence knowledge gives any additional improvement. 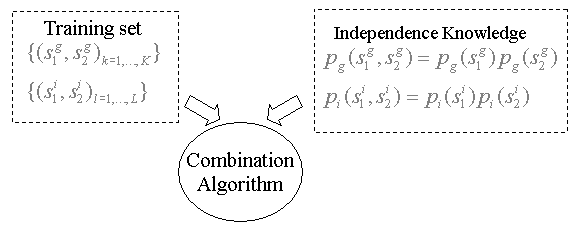The problem is really a machine learning problem: given the same number of training samples, can we reduce the learning error of the algorithm if independence knowledge is used? The training set does not provide independence knowledge; instead it should be communicated separately to the combination algorithm.
The independence knowledge allows us to decompose score densities into 1-dimensional components. Thus, instead of training M-dimensional densities, we can train 1-dimensional densities, and multiply them afterwards. The question is whether such approach have any benefits.
