[Up]
Spatial Syntax Analysis
Purpose: This analysis method is designed to identify the topology of social relationships, how people are organized in space. It is adapted from Hillier and Hanson's Gamma Analysis as described in The Social Logic of Space . It can be used to see who inhabits positions of power and who does not. It can also be used to understand the accessibility of individuals to each other and the degree of freedom in circulation between points.
Definitions:
The syntax of space, i.e. the organization of its individual units, determines the relationships between individuals in a social unit. Spatial relations influence the level of access between individuals and the level of control each can have over one another.
Inhabitants are those in whom power is vested, i.e. the controllers, whereas visitors are those who enter and stay as subjects of the controllers. In some cases ("reversed buildings" like prisons), the visitors may actually spend more time in the building than the inhabitants.
The carrier is the context outside the boundaries of the system being graphed, e.g. the exterior of a building.
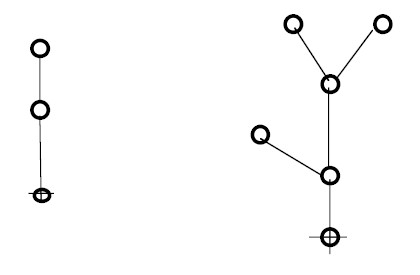
A justified graph is a diagramming technique for revealing the topology of a spatial organization. A justified graph organizes the spaces in a building in relationship to each other with the carrier at the bottom and the other spaces arranged in rows above corresponding to the number of steps in from the carrier.
Graphing conventions:
- the carrier represented by a single point (0)
- each space represented by a point (numbered 1-n)
- physical connections through doors and passageways are diagrammed as solid lines between two spaces (points)
- visual connections through openings or interior windows are diagrammed as dotted lines
- stairways are considered individual spaces
Types of spatial relationships:
Asymmetrical spatial relationships
• Two or more spaces (points) have indirect relationships with each other
• Leads to "tree-like" graphs
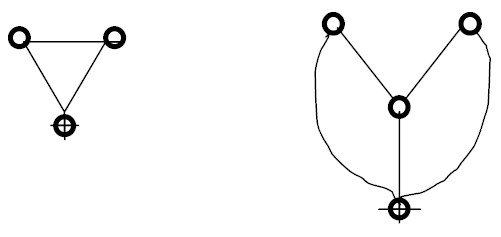
Symmetrical spatial relationships
• Two or more spaces (points) have direct relationships with each other
• Leads to "ringy" graphs
Spatial syntax calculations:
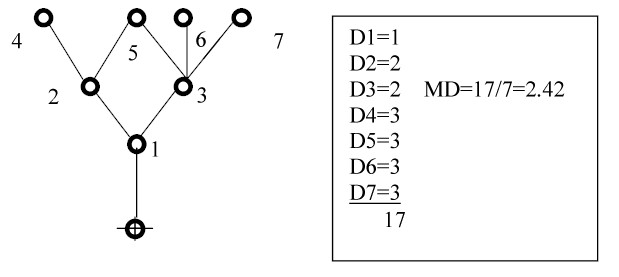
1. Depth
• Number of lines to a point from the "carrier" or any other point of reference
• Calculate by counting the number of steps (solid lines) in from the carrier
• Calculation of mean depth:
MD = (d1+d2+d3....dn)/(P-1)
where
MD is mean depth
dn is the depth of a point
P is the total number of points, including the "carrier
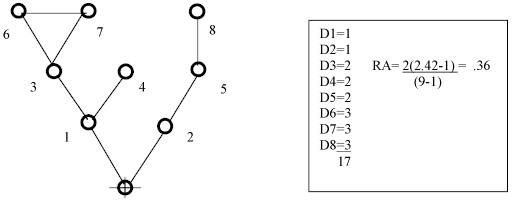
2. Relative Asymmetry
• Measure of tree-like quality of a justified graph
• Calculation:
RAn= 2(MD-1)/(P-1)
• Can be calculated from any point
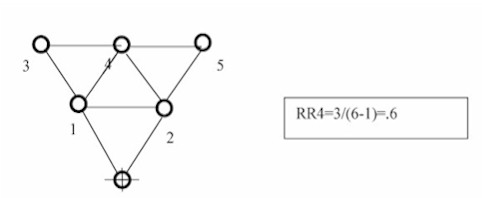
3. Relative Ringiness at a Point
• Measure of ringiness for any point on a justified graph
• Calculation:
RRn= R/(P-1)
where
RRn is the relative ringiness at a point
R is the number of independent rings passing through a point; an independent ring shares only one link with other rings
P is the total number of points in the graph, including the carrier
4. Control
• Each space has n neighbors
• Each space gives 1/n control to each neighbor
• The control value (E) for any point is the sum of values for each receiving space
• Examples below:
Patterns of spatial organization to consider in the analysis:
- level of control over access along the links
- territorial control over links to the carrier
- visual/auditory links providing control without contact and can subvert or reinforce the physical topology
- "shallow" buildings are the more socially integrated with the community (carrier) than "deep" buildings
- "shallow buildings" have more dense traffic
- tree-like buildings have more opportunities for social control
- the deeper the point, the greater the power of the inhabitant
- in "inverted buildings", power relationships are reversed and spaces are highly segregated between inhabitant and visitor, e.g. prison
Analysis steps:
- Determine the carrier and the boundaries of the system to be mapped
- Obtain or draw a plan of the building or area (does not have to be to scale)
- Overlay a graph of spaces and connections on top of the plan (physical links only)
- Justify the graph by organizing points in steps in from the carrier or other point of reference
- Compute statistics on depth, asymmetry, ringiness, etc.
- Consider the impact of visual/auditory links
- Repeat using different orientations of the graph (starting at different points) to obtain alternate perspectives (e.g. different users)
Note: See example from Hillier and Hanson in the reading.
Documentation:
- plan with overlaid graph, including numbered spaces and a key of space names
- justified graphs as needed
- calculations
- descriptions of the impact of visual/auditory links
- implications that the spatial syntax has for the social life of the building
Note: comparative calculations are particularly useful in the calculations, e.g. what if the plan were organized differently? Photographs or sketches can be helpful in communication as well.
Analsyis #3:
Complete a spatial syntax diagram (justified graph) of the first floor of your case study building. Calculate the mean depth, relative asymmetry and relative ringiness. Identify the points of highest control value.
Be prepared to discuss the following in class:
- Is the building symmetrical/asymmetrical?
- Is it ringy or tree like?
- What are the key control spaces and how important are they in the use of the building?
- What are the implications of the spatial syntax for social life in the building? For the different inhabitants and visitors?
- How would you have designed it differently and why?