Ancestors |
||
| From the earliest moments
of human history, thoughtful men and women have struggled with the
tension between the continuous, ever changing stream of sensation
and the discrete and unchanging concepts with which language and memory
records it. Throughout history, there have been those who concerned
themselves more with the sensations, and those who cared more about
the concepts. Plato (ca 428 -347), for example, is the archetype of those who
favored concepts over sensations, arguing that all sensations -- all
the information we receive from the world around us through our senses
-- are errors, misinformation designed to lead us away from the truth.
The truth, according to Plato, is stable, unchanging, perfect, and cannot be learned from studying our experiences. Truth resides not in this world, but in an ideal world, a world of ideas, where only abstract, perfect and unchanging concepts --concepts like “truth”, “beauty”, “justice”, along with abstract, perfect, immaterial circles, triangles, and other perfect geometric figures. Plato suggests that we once resided in that perfect world, but were cast out due to a fundamental sin we committed in the darkest regions of the past. We are now imprisoned in this world of illusions, and we can learn nothing from observing it; rather our sensations will lead us away from the truth. The best we can hope is that we can remember something from our previous sojourn in the world of ideas, but to do so we must close ourselves off from the distractions of this world of illusion and change. Not all Greeks abided by Plato's injunction to avoid careful study of the world of experience. Aristarchus of Samos (ca 310-430 BC), for example, who is often considered the first person to suggest that the sun, and not the earth, was at the center of the solar system, developed methods to measure the size of the earth, moon and sun, and the distances among them, although his primitive instrumentation led him to underestimate these distances greatly. Aristarchus was himself a representative of a community of scientists and mathematicians including Egyptian and Babylonian astronomers, architects, and engineers who understood that measurement is always and only a process of comparison to a standard. As Edna Kramer (1902-1984) remarks, “All measurement, whether it is concerned with distance or time or weight or electric current or intelligence or beauty, is merely comparison with a standard.”1 This distinction between the platonists -- those who believe that knowledge is absolute, categorical and certain, and the scientists -- those who believe knowledge is comparative, relative and uncertain -- is the most fundamental distinction in epistemology. |
||
| Plato's World | ||
In Plato's world, knowledge,
represented by the Greek word episteme, is perfect, unchanging,
categorical and hierarchical. It is not derived from empirical study
of the world we live in, but rather recollected from our experiences
in the world of ideas before our fall from grade. The latinization
of Plato’s concept of education comes from the Latin word ducere
(to lead) and e (from, out of) expresses Plato’s belief
that knowledge is found within the mind, not in the world. Plato’s
student, Aristotle (384-322 BC), agreed with Plato that knowledge
was perfect, unchanging, categorical and hierarchical, but did not
agree that the source of knowledge was some idealized world of ideas,
but rather the world itself. Instead, Aristotle asserted that all
existing things were made of two principles; primary
matter and substantial form. Matter is restless, constantly
changing, indefinite, and has no characteristics apart from its
restlessness. Form is absolute, unchanging and perfect. It is matter
which makes a thing exist, but it is form which makes it what it
is (to ti isti, later translated to the Latin essence.) |
||
| The World of Science | ||
| In addition to the word
“episteme”, which meant a knowledge at once abstract, perfect
and unchanging, the Greeks had another word, “scia”, which
represented another kind of knowledge, the comparative, practical,
changing and relativistic knowledge one could gain about the world
of everyday experience. Both Plato and Aristotle considered this an
inferior kind of knowledge, one that was appropriate to lesser human
beings, such as tradesmen, carpenters, brickmasons, and the like,
and not to the highest men, the philosophers. It is this kind of knowledge
that is embraced by the world of science. Plato and Aristotle’s
predecessors, particularly the Sophists,
believed that no certain knowledge could come from the world of experience,
and that all knowledge about the world of experience was relative
and uncertain. In sharp contrast to the absolute, categorical and hierarchical world of Plato and Aristotle, the world of science is relative and comparative. An object is not large, but large compared to some other thing. A work of art is not beautiful in an absolute sense, but it is more or less beautiful than some standard. And men are more or less rational or more or less animal compared to other men, rather than in an absolute sense. Furthermore, the world of science, being based on observations made by fallible humans on changing and evanescent phenomena is always subject to uncertainties of measurement and subject to revision by later, more precise observations. As Einstein says, “as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality.” It goes without saying that the Platonic model, which recommends isolation from the world of experience, is not suitable to the development of an empirical science. Aristotle’s rejection of Plato’s antipathy for empirical observation was not in itself enough to overcome the problem, however, because it retains the idea that the goal of science is absolute, categorical, unchanging truth. The development of physical science as we know it required the rejection of Aristotle’s categorical, syllogistic model and the development of the comparative model. Although early Egyptian, Babylonian, Assyrian, Hindu and other architects and astronomers used comparative measurements, most writers mark the beginning of serious, self-conscious science in the modern sense with Galileo Galilei (1554-1642). Galileo’s experimental work is filled with outstanding examples of the comparative method of measurement. His experiments with buoyancy, for example, show him adding enough salt to a glass container of water so that a pea will float midway between the top and bottom of the water. Adding 1 pinch of salt will cause the pea to rise “3 finger breadths.” Here Galileo is comparing the distance the pea rises to the width of his fingers. He is alleged to have observed the swinging of chandeliers in church and timed them against his pulse beat. In his even more famous experiment with falling bodies, Galileo rolled a ball down a groove in an inclined plane. As he did so, he hummed a rhythmic song, and marked the position of the rolling ball on the beats with chalk. He then placed movable frets across the chalk marks, then rolled the ball repeatedly, adjusting the positions of the frets until the ball bumped over them exactly on the beats. He then had only to measure the distances among the frets to determine how far the ball fell in equal intervals, and from this he was able to deduce the exponential law of falling bodies. In this case he is comparing distances fallen to the rhythmic pulse of music. |
||
| Galilean Transformations and Standards of Measure | ||
The sophists believed
not only that observations and their resulting knowledge were relative,
but also that they were personal and individualistic, so that the
observations of one observer need not correspond to the observations
of any other. This radical individuality of knowledge was at the
base of the sophists' belief that no knowledge was possible, but
only opinion. The goal of science, however, is not a personal, idiosyncratic
knowledge unique to each individual, but rather a public, shared,
objective knowledge about which all observers agree. If Galileo
and another observer compare motions of any object to their respective
pulse beats, they will disagree to the extent that their pulse rates
are not the same. If the observations made while comparing some
motion to the pulse beat of the observer reveals something exciting,
the excited observer’s pulse rate will increase and change
the outcome unpredictably.
disagree solely as a result of the different orientations of their
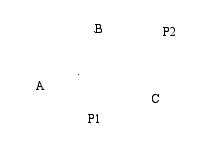
individual frames of reference. As can be seen in the figure, for
example, an observer at P1 will see, from left to right, A, B, C
in that order, while and observe e at P2 will see the array C,A,B
from left to right. These differences are solely the result of difference
of reference frame, even though both observers are viewing the “same”
three objects. |
||
| Aristotle’s Social Science | ||
| While physical scientists
following the methods of Galileo made explosive progress in describing
experience, social scientists continued to work with the antiquated
Aristotelian concepts. Since Aristotle’s model was categorical,
it could not describe processes precisely, which led to some enormous
observational errors. Aristotle theorized, for example, that objects
fell at a rate proportional to their weight, so that a heavy object
would fall faster than a light object. This, of course, is not true,
as Galileo’s law of falling bodies shows, but Aristotle’s
law stood almost 2000 years. Many writers make light of the fact that the most learned minds of Europe and Asia were unable to demonstrate that Aristotle’s Law of Falling Bodies was false for 2000 years by suggesting that air resistance can account for the discrepancy; after all, in air, a feather does fall more slowly than a hammer. But, in fact, the discrepancy between Aristotle’s law and everyday observation is enormous. Consider a paper clip that weighs half a gram, and an encyclopedia that weighs 5 kilograms. The book is 10,000 times heavier than the paper clip, and Aristotle’s law demands that it fall 10,000 times faster than the paper clip. If one lays the paper clip on top of the book, and drops the book from the height of a person standing on a desk, it will be obvious to every observer in the room that the paperclip remains in contact with the book at all times, falling at an identical velocity. See these NASA vids showing objects dropped in space too. How could this extraordinary disagreement between theory and observation survive 2000 years? Could it just be that no one made any observations of falling bodies? Absolutely not. In 1066, at the Battle of Hastings, gunpowder was introduced into Western warfare. For the following 500 years, military research enlisted the best minds of Europe in the analysis of the trajectory of mortar rounds and artillery shells. Yet it was Galileo who determined that the trajectory of a projectile was parabolic, almost six hundred years later. It is unlikely that the military researchers were unmotivated or unintelligent over that 500 plus year period. Much more likely is that the new comparative methods of Galileo made it possible to see phenomena that were not accessible to those using an Aristotelian categorical model. |
||
| The Comparative Model | ||
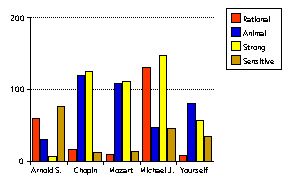
| To illustrate the difference
between the Aristotelian categorical model and the comparative scientific
model, consider the following definition of several men. In the following
questionnaire, respondents are asked to report how dissimilar or “far
apart” some men and attributes are from each other. Since all
measurement is the comparison to some standard, respondents are told
to use the distance between sensitive and strong as a standard dissimilarity,
and to estimate all other dissimilarities as ratios to that standard.
The result is a square matrix of dissimilarities which can be converted
to a spatial representation by well known mathematical procedures. |
||
|
|
||
| Instructions Please estimate how different or "far apart" each of the following words or phrases is from each of the others. The more different, or further apart they seem to be, the larger the number you should write. To help you know what size number to write, remember SENSITIVE AND STRONG ARE 100 UNITS APART If two words or phrases are not different at all, please write zero (0). If you have no idea, just leave the space blank. Thank you very much for your help. ---------------------------------------------------------- SENSITIVE AND STRONG ARE 100 UNITS APART COL. ---------------------------------------------------------- 0102 9-17 RATIONAL and ANIMAL _____ 0103 18-26 RATIONAL and STRONG _____ 0104 27-35 RATIONAL and SENSITIVE _____ 0105 36-44 RATIONAL and ARNOLD S. _____ 0106 45-53 RATIONAL and CHOPIN _____ 0107 54-62 RATIONAL and MOZART _____ 0108 63-71 RATIONAL and MICHAEL J. _____ 0109 72-80 RATIONAL and YOURSELF _____ ---------------------------------------------------------- SENSITIVE AND STRONG ARE 100 UNITS APART COL. ---------------------------------------------------------- 0203 9-17 ANIMAL and STRONG _____ 0204 18-26 ANIMAL and SENSITIVE _____ 0205 27-35 ANIMAL and ARNOLD S. _____ 0206 36-44 ANIMAL and CHOPIN _____ 0207 45-53 ANIMAL and MOZART _____ 0208 54-62 ANIMAL and MICHAEL J. _____ 0209 63-71 ANIMAL and YOURSELF _____ 0304 72-80 STRONG and SENSITIVE _____ ---------------------------------------------------------- SENSITIVE AND STRONG ARE 100 UNITS APART COL. ---------------------------------------------------------- 0305 9-17 STRONG and ARNOLD S. _____ 0306 18-26 STRONG and CHOPIN _____ 0307 27-35 STRONG and MOZART _____ 0308 36-44 STRONG and MICHAEL J. _____ 0309 45-53 STRONG and YOURSELF _____ 0405 54-62 SENSITIVE and ARNOLD S. _____ 0406 63-71 SENSITIVE and CHOPIN _____ 0407 72-80 SENSITIVE and MOZART _____ ---------------------------------------------------------- SENSITIVE AND STRONG ARE 100 UNITS APART COL. ---------------------------------------------------------- 0408 9-17 SENSITIVE and MICHAEL J. _____ 0409 18-26 SENSITIVE and YOURSELF _____ 0506 27-35 ARNOLD S. and CHOPIN _____ 0507 36-44 ARNOLD S. and MOZART _____ 0508 45-53 ARNOLD S. and MICHAEL J. _____ 0509 54-62 ARNOLD S. and YOURSELF _____ 0607 63-71 CHOPIN and MOZART _____ 0608 72-80 CHOPIN and MICHAEL J. _____ ---------------------------------------------------------- SENSITIVE AND STRONG ARE 100 UNITS APART COL. ---------------------------------------------------------- 0609 9-17 CHOPIN and YOURSELF _____ 0708 18-26 MOZART and MICHAEL J. _____ 0709 27-35 MOZART and YOURSELF _____ 0809 36-44 MICHAEL J. and YOURSELF _____ ---------------------------------------------------------- |
||
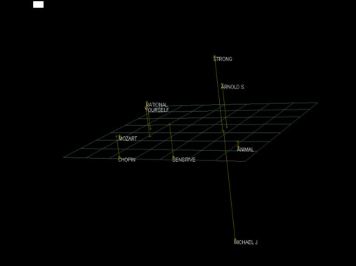
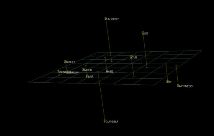
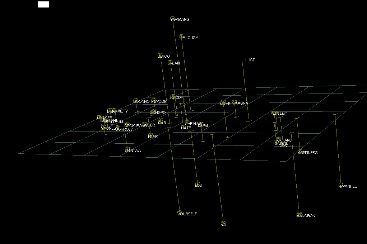
| Figure 2 is the spatial
representation of responses to the questionnaire constructed by the
Galileo
computer program and displayed with ThoughtView™
The dimensions (x,y and z) are the principle axes of the configuration
of points. In the map shown in Figure 2, objects are close to other
objects that are like them, and far from objects from which they differ.
Direction (up, down, left right, in, out) is of no significance. The
grid is supplied only to help visualize the distances among the objects,
and has no other significance. The orientation of the space is also
of no significance, so it doesn’t matter which objects are at
the top, or how far from the grid they are. The inter point distances
are invariant under rotation, translation and reflection, so turning
the space upside down or sideways does not affect it’s meaning.
In these maps, as with the map of men
and their attributes, the respondents are closer to the emotions
to the extent that they are experiencing them, and the emotions
are close to other emotions that are similar to them and far from
those that are seen to be different. Within each map it is therefore
possible to compare each emotion to every other emotion, and to
see the relationship of the individual (MYSELF or MA) to each of
the emotions.
|
||
1 Kramer, Edna E., The Main Stream of Modern Mathematics, The Scholar’s Bookshelf, Princeton, NJ, 1988, p.42 2 “True” differences are differences not due to effects of differential reference frames, and not “true” in a platonic sense. page updated May 30, 2012 |
||
 ,
therefore Arnold, Michael, Frederick and Wolfgang are also members
of
,
therefore Arnold, Michael, Frederick and Wolfgang are also members
of the category “mortal”.
the category “mortal”. extent
to which each of these men exhibits the characteristics of manhood,
since the system is absolute and categorical. The form “man”
in Aristotle’s system has the attributes “rational”
and “animal.” Insofar as he is a man, every man is identically
rational and animal. The form “man” is unchanging and
perfect. We abstract the meaning of “man” from our observation
of many individual men, and, although the restlessness of the primary
matter which establishes their existence obscures the perfection
and changeless nature of the form “man,” we are able to
form a concept of the pure form independent of its manifestation
in any individual.
extent
to which each of these men exhibits the characteristics of manhood,
since the system is absolute and categorical. The form “man”
in Aristotle’s system has the attributes “rational”
and “animal.” Insofar as he is a man, every man is identically
rational and animal. The form “man” is unchanging and
perfect. We abstract the meaning of “man” from our observation
of many individual men, and, although the restlessness of the primary
matter which establishes their existence obscures the perfection
and changeless nature of the form “man,” we are able to
form a concept of the pure form independent of its manifestation
in any individual.