The Galileo Group at Albany

As evidence for the non-Euclidean character of cognitive maps grew, the psychometric community continued to struggle with methods to force euclidean solutions. One particularly troublesome dataset that made the rounds of developers was the “tea tasting data”. No known MDS program in the psychometric community could solve the tea tasting data, for a simple reason: people like hot tea, and they like iced tea, but most people do not like tepid tea. In a cognitive space, this means that the ideal point -- the point most preferred -- must lie close to iced tea, and close to hot tea, but not close to tepid tea, which, of course, lies between iced and hot tea. This is not possible in any euclidean space, but is simple in a riemann space which is warped so that iced tea and hot tea are closer to each other than they are to tepid tea. The Galileo program, using classical Young Householder Torgerson methods, solves this problem exactly.

The sizes problem

The first Galileo ever made was a picture of Alice in Wonderland. Students were asked to estimate the distances between objects in the picture, and the general form of the picture could be reproduced from the Galileo coordinates. What the picture made graphically evident was that the objects in the picture, unlike the ideal points in hypothetical multidimensional scaling spaces, were not points at all, but objects that had shapes and occupied volume in three dimensional space.
When Barnett first estimated the reliability of Galileo solutions, he noted the presence of reliable negative eignevalues, an indication that the Galileo space was non-euclildean. In the early 1970s, high dimensional, non euclidean spaces were anathema, even to the Galileo researchers, and Barnett speculated that the non-euclidean components of the space might be attributable to the error introduced by treating the objects as points rather than measuring the sizes of the objects and including these in the interpoint distance matrix.

Joseph and Robert Prusek considered this argument again at Albany in the early 1980’s. They constructed 32 examples, each of which consisted of between 4 and 20 circles of varying radii, and measured the distances among their perimeters. This indeed resulted in non euclidean spaces. They then investigated two mathematical solutions for recovering the radii from information contained in the imaginary part of the spaces. They found that “...both methods work reasonably well in most cases, and very well in some cases, although four cases exist in which correlations between the estimated radii and the true radii are essentially zero.”

The Albany Research Organization

Galileo research, first at Illinois and then at Michigan State, was generally loosely organized, unfunded and based on volunteer student effort, using large undergraduate classes as experimental subjects and field researchers. In the days before the personal computer, the computationally and data intensive Galileo research program coordinated the inputs of manystudents through the University’s Sperry-Univac mainframe computer. Research groups of about five students, each with a supervisor who reported to a higher level supervisor (“hypervisor”) conduted telephone interviews, administered experiments and questionnaires, and entered data into the Sperry-Univac using special software written by Richard A. Holmes,


Rob Zimmelman, Scott Danielsen, Joseph Woelfel and others. This organization had considerable capacity, and conducted several statewide and even national studies, including tracking of a NY gubenatorial campaign and the 1988 Presidential election.
These campaigns supported Barnett et. al. in hypothesizing that the relative distances of the candidates from the self point were highly predictive of the outcome. A program written in Australia by Roger Wilkinson counted the number of respondents closer to each candidate, and this percentage predicted the vote in New York State to within 1% in both elections, while national pollsters missed the gubernatorial in NY be double digits. 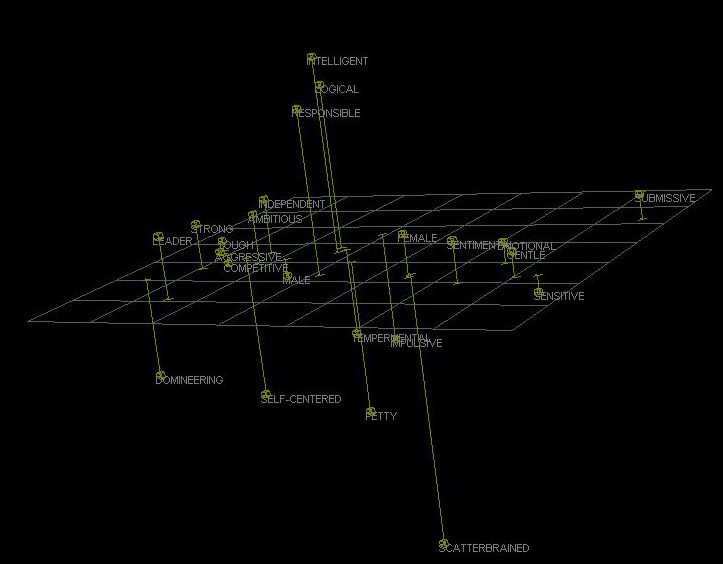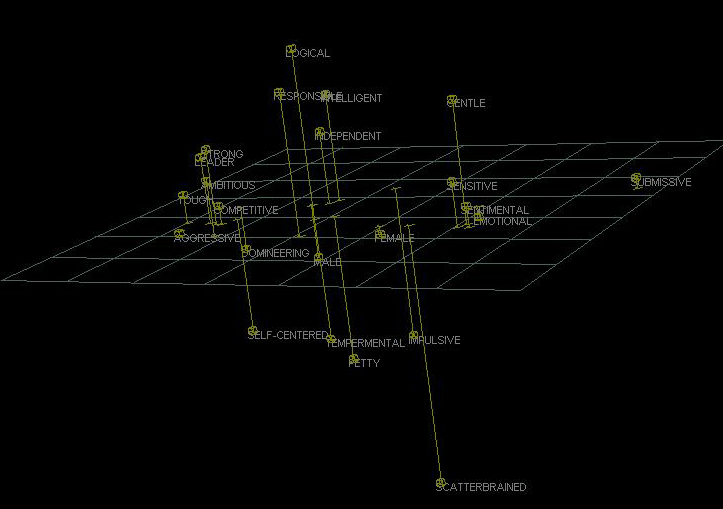The precision of measure of the Galileo for political research is evident in the comparison of men (left) and woman in the1988 presidential election in New York:




In order to simplify the coordination of the student researchers, a shell was constructed which intercepted the mainframe logon of the students. This shell (SPOT) evolved into a quasi-intelligent system which Scott Danielsen is going to describe with exquisite skill very soon.