In a 1987 paper, "The Delayed Impacts of Plant Closures in a Reformulated Leontief Model", I showed that the time-varying impacts of changes to a regional economy can be calculated using a simple elaboration of the Leontief inverse model. In a critique of this paper "Closure in Cole's reformulated Leontief Model" R. W. Jackson, M. Madden, and H. A. Bowman complained that they were unable to reproduce my results. I provided them with a step-by-step demonstration of the method and showed that their failure lies in their treatment of the external (rest-of-world) sector. The calculation is quite simple - it requires a single matrix inversion and requires no sub-matrix multiplication. Nor does it require as many arbitrary assumptions as the "conventional" input-output model. Thus, the model can be explained simply as the result of a common-sense round-by-round multiplier process. I have applied the method in a variety of situations, for example, to calculate the shifts in community income and its distribution following a major catastrophe. I illustrate the method using a single or multi-region social accounting matrix. In the example I use a simple local region-rest of the world set of social accounts.

Social Accounts

The approximation for the calculation of time-lagged economic impacts is

where X(T) is a vector of impacts at a time horizon T, Q(T) are the marginal expenditures, A is a matrix of coefficients, for a single economy or a multi-regional system, and P(T) is the distribution of initial events Y. The time dependent multipliers M(T) are calculated from the denominator of this expression. The steps for carrying out this calculation are given in the spreadsheet that can be downloaded from this site. The steps in the calculation are as follows:

• Step 1 shows the stylized aggregate social accounts. This includes supply-side (all production activities), demand-side (households, government, and investment demand), and rest-of-world transactions (trade and finance).
• Step 2 gives the consumption propensities. This is the A-matrix referred to in the formula above with the spreadsheet equations.
• Step 3 introduces the time horizon, transaction delays and rest-of-world feedback. Since lags occur for a variety of reasons (technical, financial, institutional) they vary across actors.Changes in the domestic economy (supply or demand) stimulate the external economy, and in turn there will be some feedback from this to the local economy. In the calculation, this feedback is represented by a parameter d.
• Step 4 gives the marginal propensities at time T given by the A matrix multiplied by the Q(T) and d. Step 5 sets up the modified Leontief matrix. In practical calculations Steps 2 to 5 may be combined.
• Step 6 uses a standard inversion routine on the modified Leontief matrix to obtain the matrix of multipliers M(T). Multipliers for more elaborate tables may be calculated using the same procedure, i.e. inversion of a single matrix. with no sub-matrix manipulation.

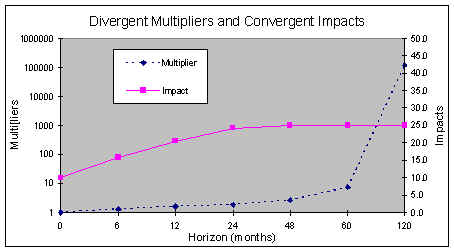
In my response to Jackson et al I considered the case of the same region embedded in a closed model of the entire world economy. I noted the divergent growth in the regional multipliers of this system at long time horizons, but showed that these multipliers are unperturbed at the short- to medium-run horizons of typical of input-output calculations. In a new paper "Closing the Case on Closure in Cole's Model", Jackson and Madden say that the role of the distribution of lags was never in question. This said, they proceed to formalize a model for the situation of a regional economy interacting with the entire world economy but only for the case of an infinite time horizon. Predictably, they then discover that the multipliers necessarily must diverge. Although their model is inconsistent, it raises an interesting question about the possibility of infinite multipliers in a finite system.

I have examined this paradox in a new paper, "The Phantom of the Matrix" (Papers in Regional Science, 78, 429-436, 1999). This paper presents an exact solution to my original model for the infinite time horizon equilibrium case and directly rebuts the complaints of Jackson and Madden. It argues that, for the class of demand-driven economic-base models to which input-output models belong, injecting all sectors with a vector of exogenous demand equal to their export earnings should reproduce the equilibrium output of all sectors. With no injection, the economy should shrink to zero. Unless this critical test of internal consistency is fulfilled, any demand-driven input-output model -- lagged or unlagged -- cannot be expected to provide reliable results for any other injection. This prerequisite is satisfied by my solution to the lagged model recognizing that, for a fully closed system, there can be no net exogenous demand or leakage. As far as I can tell, the condition is not satisfied by other current input-output solutions.

This solution resolves the seeming paradox of infinite multipliers in a finite totally closed economy. Consider the situation of a small region embedded in the rest-of-the-world economy. This is a closed system, at least in a narrow economic sense. (In an ecological sense it is not closed - we receive a steady supply of sunlight, meteoric minerals, and little green men.) At an infinite time horizon all activities throughout the world will be fully stimulated by even the smallest exogenous disturbance to the regional economy. The multiplier is infinite. But this does not mean that the world economy will explode. Since the real world economy is unambiguously closed, exogenous demand for any place is offset exactly by an exogenous net demand elsewhere in the rest of the world. Put simply, there is no net exogenous demand for the multiplier to multiply. 

Download the Lagged Input-Output Model

Return to Sam Cole's Home Page