Simple Linear Image Classifier¶
How about computing the average of all the "8"s, of all the "4"s, etc.? Let's see what we get.
If we form the dot product of the average of the "4"s with a single image, we might expect that dot product to be large if the image is a 4 and smaller if it isn't a 4. Let's take a look.
In [2]:
from glob import glob
from PIL import Image
from numpy import *
import matplotlib.pyplot as pl
import os
%pylab inline
# we will compute the mean character of the images for each class
imagefolder = 'mean_character_images/'
if not os.path.exists(imagefolder):
os.makedirs(imagefolder)
allpngs = glob('pngs/*.png')# set of all pictures names
# exctracts label for a given picture
def get_class(png): return png[-6:-4]
# list of character classes
classes = list(set([get_class(png) for png in allpngs]))
print(classes)
In [3]:
sampleimg = Image.open(allpngs[0])
imshow(sampleimg)
h,w,nc = array(sampleimg).shape
print( array(sampleimg).shape )# height width layers
Let's compute the the average image for each class¶
In [4]:
# Training step
class_averages = {}# empty dictionary of form: character_class, average_image
for character_class in classes:
# list of pngs in this character_class
pngs = [png for png in allpngs if get_class(png)==character_class]
print(character_class,len(pngs))
# go through all images for a given class and add together the pngs pixel-by-pixel
average_image = zeros((h,w),dtype=float)#empty image to start
for png in pngs:
a = 255-array(Image.open(png))[:,:,0] # select just the red channel (and invert)
average_image += a
average_image -= average_image.mean()# normalize the images by subtracting off their means
# save the mean image to a .png file
pl.imsave(imagefolder+'average_'+character_class+'.png',average_image,vmin=average_image.min(),vmax=average_image.max(),cmap='seismic')
# save the average_image into a dictionary
class_averages[character_class] = average_image
#ad['_0'].max()
The shifted averages of each character class:¶
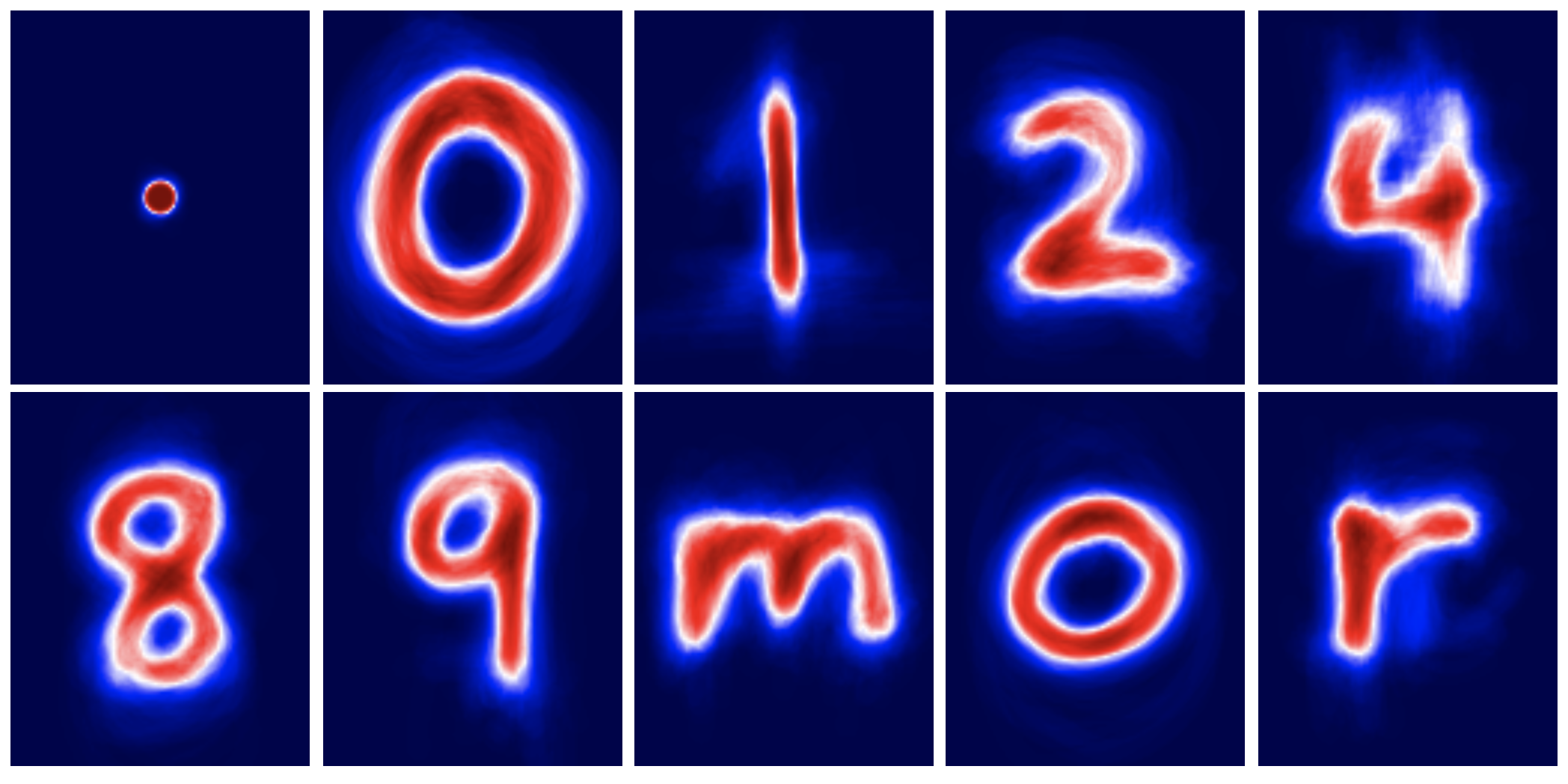
Given these averages for character recognition, we can try a simple approach to image classification:¶
- Compute the dot product between a given image (treating it as a vector) and the average image for each image class
- Classify each image as the the character class for which the dot product is the greatest
In [5]:
# testing part
for character_class in classes:
# list of pngs in this class
pngs = [png for png in allpngs if get_class(png)==character_class]
#print(sig,len(pngs))
predicted_labels = []
for png in pngs:
the_image = 255-array(Image.open(png))[:,:,0] # select just the red channel (and invert)
dot_products = []
for class2 in classes:
dot_products.append((the_image*class_averages[class2]).sum())# compute dot product
predicted_label = argmax(dot_products)
predicted_labels.append(predicted_label)
ncorrect = sum([classes[predicted_label]==character_class for predicted_label in predicted_labels])
print('{:2} {:4d} of {:3d}, {:2.1f}% correct'.format(character_class,ncorrect,len(pngs), ncorrect/len(pngs)*100))
Not bad, but can we do better? What if we computed weighted dot products. That is, perhaps the averages are not the best images to multiply by.¶
In [6]:
def compute_mean_error(Weights):
frac_correct = 0
for character_class in classes:
# list of pngs in this class
pngs = [png for png in allpngs if get_class(png)==character_class]
#print(sig,len(pngs))
predicted_labels = []
for png in pngs:
a = 255-array(Image.open(png))[:,:,0] # select just the red channel (and invert)
dot_products = []
for class2 in classes:
dot_products.append((a*class_averages[class2]*Weights).sum())# compute dot product for matrices
predicted_label = argmax(dot_products)
predicted_labels.append(predicted_label)
ncorrect = (sum([classes[predicted_label]==character_class for predicted_label in predicted_labels]))
#print('{:2} {:4d} of {:3d}, {:2.1f}% correct'.format(character_class,ncorrect,len(pngs),ncorrect/len(pngs)*100))
#print(frac_correct)
frac_correct += ncorrect/len(pngs)/len(classes)
frac_error = 1 - frac_correct
return frac_error
In [7]:
Weights = ones((h,w)) # there are 125*100 coefficients to tune
frac_error = compute_mean_error(Weights)
print(frac_error)
In [8]:
for k in range(40):
#print(k)
Weights_new = Weights + .1*random.random((shape(Weights) ))
frac_error_new = compute_mean_error(Weights_new)
if frac_error_new < frac_error:
print(frac_error_new,k)
Weights = Weights_new
frac_error = frac_error_new