SPARCS¶
SPARCS data (see here for info)
In [1]:
import pandas
In [2]:
# cleaning the data
mycons = {'Total Costs':lambda x:float(x.replace('$','')),
'Total Charges':lambda x:float(x.replace('$','')),
'Length of Stay':lambda x:int(x.replace('+',''))}
s = pandas.read_csv('sparcs2014.csv',converters=mycons)
s.head()
Out[2]:
In [3]:
pop2014 = 19.75e6
int(s['Total Charges'].sum()/pop2014)
Out[3]:
In [4]:
print(s['Total Charges'].max())
print(s['Total Costs'].max())
In [5]:
itcmax = s['Total Charges'].idxmax()# index of row in which the charages are the highest
s.iloc[itcmax] # get data in row for the most expensive hospital visit
Out[5]:
In [6]:
itcmin = s['Total Charges'].idxmin()
s.iloc[itcmin] # get data in row for the least expensive hospital visit
Out[6]:
In [7]:
meantc = s['Total Charges'].mean()
meantc
Out[7]:
In [8]:
mediantc = s['Total Charges'].median()
mediantc
Out[8]:
In [9]:
from histogram1d import histogram1d
In [10]:
len(s)
Out[10]:
In [11]:
from numpy import *
def histogram1d(xall,xmin,xmax,nbinsx=10,rawcounts=False):
xfac = float(nbinsx)/float(xmax-xmin)
inbox = logical_and(xall>=xmin,xall<xmax);
x = xall[ inbox ]
ix = array( (x-xmin)*xfac, dtype=int )
counts = zeros(nbinsx,dtype=int)
add.at( counts, ix, 1 )
dx = (xmax-xmin)/float(nbinsx)
#bincenters = linspace(xmin,xmax,nbinsx+1)[:-1]+0.5*dx
left = linspace(xmin,xmax,nbinsx+1)[:-1] # left ends of bins
if rawcounts:
#return bincenters,counts
return left,counts
else:
# return probability density samples
#return bincenters, counts/(dx*float(len(xall)))
return left, counts/(dx*float(len(xall)))
In [12]:
mincharge = s['Total Charges'].min()
maxcharge = s['Total Charges'].max()
lefts,p = histogram1d(s['Total Charges'],mincharge,maxcharge,100)
lefts
Out[12]:
In [13]:
%pylab inline
bar(lefts,p,lefts[1]-lefts[0],color='m',alpha=0.4)
Out[13]:
In [14]:
lefts,p = histogram1d(s['Total Charges'],mincharge,maxcharge/100,100)
In [15]:
bar(lefts,p,lefts[1]-lefts[0],color='m',alpha=0.4) # bar widths
Out[15]:
In [16]:
lefts,p = histogram1d(log10(s['Total Charges']),log10(mincharge),log10(maxcharge),100)
bar(lefts,p,lefts[1]-lefts[0],color='m',alpha=0.4)
Out[16]:
In [17]:
lefts,p = histogram1d(log10(s['Total Charges']),3,6,100)
bar(lefts,p,lefts[1]-lefts[0],color='m',alpha=0.4)
xlabel('log(total charges)')
ylabel('probability')
Out[17]:
This data looks log normal¶
Let's fit a Gaussian distribution to this data¶
In [18]:
def gaussian(x,mu,sigma):
return (1/sqrt(2*pi)/sigma)*exp(-(x-mu)**2/2/sigma**2)
In [19]:
lc = log10(s['Total Charges'])#log charges
lefts,p = histogram1d(lc,3,6,100)
w = lefts[1]-lefts[0] # width or step size
bar(lefts,p,lefts[1]-lefts[0],color='m',alpha=0.4)
mu = lc.mean() # mean of lc
sigma = lc.std() # standard devtiation of lc
plot(lefts+w/2,gaussian(lefts+w/2,mu,sigma),'r',lw=3,alpha=0.5) # plots gaussian with same mean and std
Out[19]:
Often, when making histograms we try to find a happy medium between low resolution (too few bins) and noisy bin heights (too many bins). This is appropriate when the data values are believed to be essentially random numbers with a probability density that varies slowly on the scale of bins.
In [ ]:
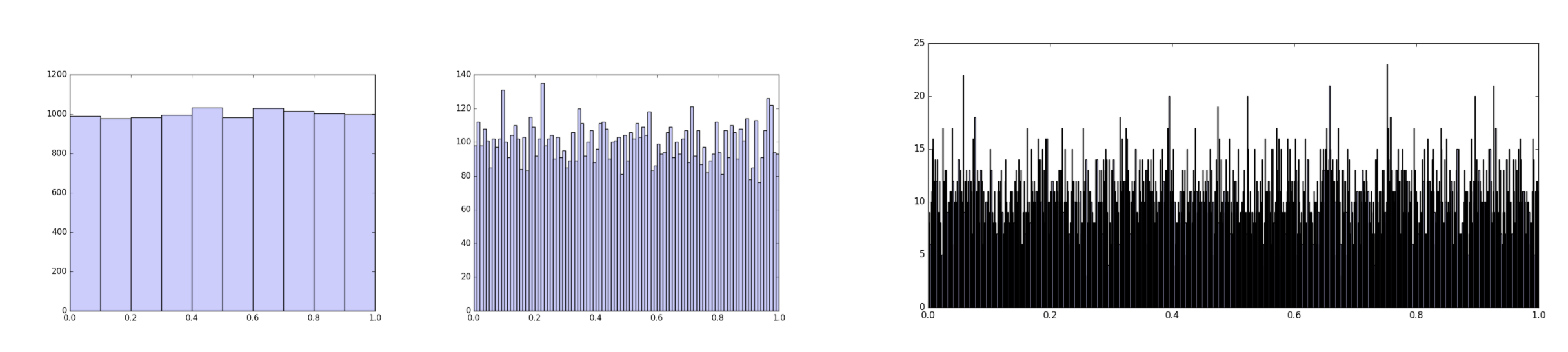
from numpy import *
from histogram1d import histogram1d
import matplotlib.pyplot as pl
N = 10000
x = random.rand(N)
pl.ion()
while True:
n=int(input('n = '))
if n<=0: break
print('N/n = ',round(N/n,1),'sqrt(N/n) = ',round(sqrt(N/n),1),'sqrt(N/n)/(N/n) = ', sqrt(N/n)/(N/n) )
lefts,counts = histogram1d(x,0,1,n,rawcounts=True)
w = lefts[1]-lefts[0]
pl.clf()
pl.bar(lefts,counts,w,color='#ccccff')
pl.xlim(0,1)
pl.draw()
pl.ioff()
input()
Mean bin occupancy: 1000, 100, 10 respectively (data the same for all 3 cases):
Quiz: "bin size": What should the average bin occupancy be so that the noise is about 5%?
[Poisson variance is N/n. Binomial variance is (N/n)(1-1/n) ~ N/n.]
But other times, like the present context of hospital charges, a very fine grain may be appropriate, and large differences in adjacent bar heights can be real and meaningful.
Exercise: Make a very fine-grained histogram of the log10 of the charges for "LIVEBORN" at Maimonides Medical Center.
In [ ]:
mmc = s[ s['Facility Name']=='Maimonides Medical Center' ]
mmcbabies = mmc[ mmc['CCS Diagnosis Description'] == 'LIVEBORN' ]
babylogcharges = log10(mmcbabies['Total Charges'])
babymax = babylogcharges.max()
babymin = babylogcharges.min()
from histogram1d import histogram1d
import matplotlib.pyplot as pl
lefts, counts = histogram1d(babylogcharges, babymin,babymax, 10000, rawcounts=True)
w = lefts[1]-lefts[0]
values = lefts + w/2
x = vstack([values,values])
y = vstack([zeros_like(counts), counts])
pl.figure(figsize=(12,6))
pl.plot(x,y,'b')
pl.show()
In [ ]:
a = s['Patient Disposition']
g = s.groupby('Patient Disposition')
for name,item in g:
print(name)
In [ ]:
g['Patient Disposition'].count()
In [ ]:
g['Total Charges'].mean()
In [ ]:
len(unique(s['Patient Disposition']))