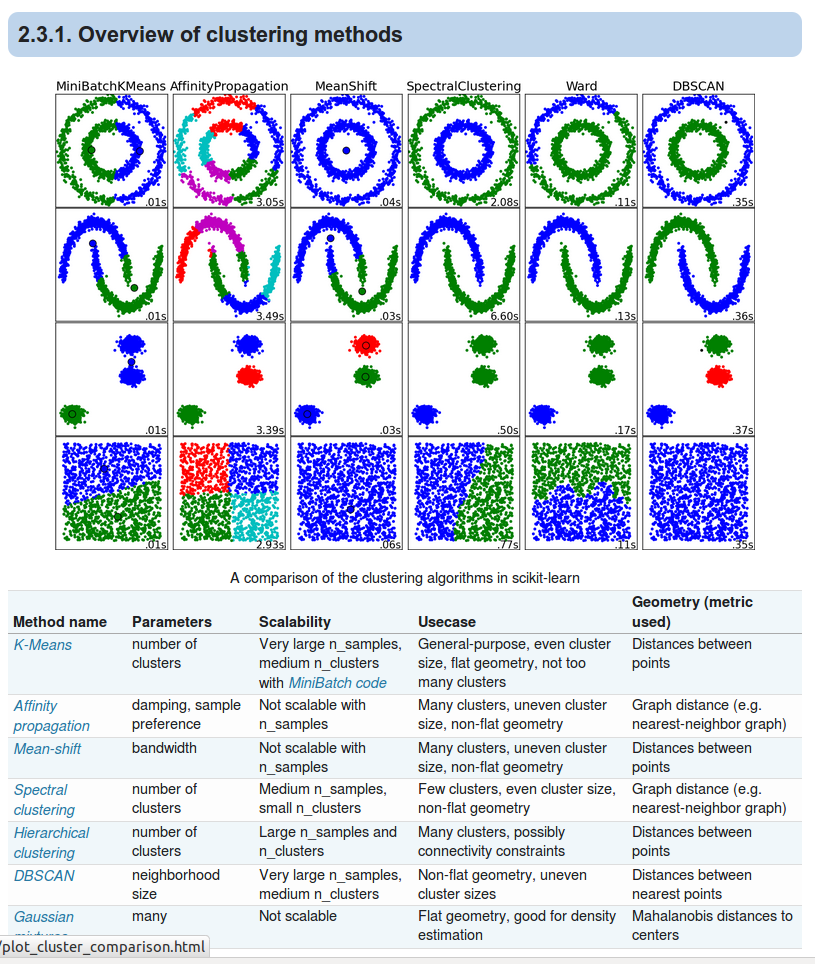
Recap of k-Means - Unsupervised clustering¶
Recall that the kmeans aims to partition points into clusters and assign each group a mean (or center) so that each point is assigned to the nearest center and each center represents the average location of the points in its cluster.
We observed previously that the results are very sensitive to initial condition. For example, consider...
In [289]:
import matplotlib.pyplot as pl
from time import sleep
import os
from numpy import *
In [290]:
def create_clustered_data(d,k,npercluster,r):
n = k*npercluster # total number points
# generate random points in unit square that are at least 2r apart
centers = [random.rand(d)]
while len(centers)<k:
trialcenter = random.rand(d)
farenough = True # optimistic!
for center in centers:
if linalg.norm(trialcenter-center,inf) < 2*r:
farenough = False
break
if farenough: centers.append(trialcenter)
centers = array(centers)
F = empty((n,d))
for i in range(k):
# create a cluster
start = i*npercluster
stop = (i+1)*npercluster
F[start:stop,:] = centers[i] + r*(2*random.rand(npercluster,d)-1)
return F,n
def plot_data_and_means(F,k,means,assignments):
colors = 'rgbmc' # red, green, blue, magenta, cyan
for i in range(k):
cluster = assignments==i
pl.plot(F[cluster,0],F[cluster,1],'.',color=colors[i],alpha=0.95);
pl.plot(means[i][0],means[i][1],'o',color=colors[i],markersize=50,alpha=0.1)
pl.plot(means[i][0],means[i][1],'.',color='k')
pl.xlim(-r,1+r); pl.ylim(-r,1+r)
return
In [291]:
def initialize_kmeans(F,k):
means = F[random.choice( range(n), k, replace=False )]
displacements = F[:,:,newaxis] - means.T # create 3D array (done after class)
sqdistances = (displacements**2).sum(axis=1) # Euclidean distance
assignments = argmin( sqdistances, axis=1 )
return means,assignments
In [292]:
def run_kmeans(F,k,max_iterations):
n=shape(F)[0]
oldassignments = k*ones(n,dtype=int)
count = 0
while(True):
count += 1
if count>max_iterations: break
# compute the cluster assignments
displacements = F[:,:,newaxis] - means.T # create 3D array (done after class)
sqdistances = (displacements**2).sum(axis=1)
assignments = argmin( sqdistances, axis=1 )
#print(assignments)
if all( assignments == oldassignments ): break
oldassignments[:] = assignments
# update the means as the centroids of the clusters
for i in range(k):
means[i] = F[assignments==i].mean(axis=0)
return means,assignments
In [300]:
# Run kmeans experiment
d,k,npercluster,r,max_iterations = 2,5,25,0.05,100
F,n = create_clustered_data(d,k,npercluster,r)
means,assignments = initialize_kmeans(F,k)
means,assignments = run_kmeans(F,k,max_iterations)
plot_data_and_means(F,k,means,assignments)
Let's improve the initialization by choose the most distant points for the initialization¶
In [308]:
center = zeros(k,dtype=int)
center[0] = random.randint(n)# at first, center will contain the ids for the 5 initial points
#print(center)
x = zeros((n,k)) # this is a vector of distances
#print(F[center[i],:] - F)
for i in range(k-1):
x[:,i] = sum(square(F[center[i],:] - F),axis=1)# matrix in which entry j,i contains distance from node j to center i
plot(x[:,i])
center[i+1] = argmax(amin(x[:,0:(i+1)],axis=1))# returns the id of the point that is farthest from the previously selected centers
#center
center = F[center,:]# convert the point ids to the point locations
center
#print(x)
Out[308]:
In [309]:
# package the above code into a function
def initialize_kmeans(F,k):
center = zeros(k,dtype=int)
center[0] = random.randint(n)
x = zeros((n,k))
for i in range(k-1):
x[:,i] = sum(square(F[center[i],:] - F),axis=1)
#plot(x[:,i])
center[i+1] = argmax(amin(x[:,0:(i+1)],axis=1))
means = F[center,:]
displacements = F[:,:,newaxis] - means.T # create 3D array (done after class)
sqdistances = (displacements**2).sum(axis=1) # Euclidean distance
assignments = argmin( sqdistances, axis=1 )
return means,assignments
In [318]:
# Run kmeans experiment
d,k,npercluster,r,max_iterations = 2,5,25,0.05,100
F,n = create_clustered_data(d,k,npercluster,r)
means,assignments = initialize_kmeans(F,k)
means,assignments = run_kmeans(F,k,max_iterations)
plot_data_and_means(F,k,means,assignments)
That works! Basically every time!¶
How might we measure the performance of k-means:¶
- Measure each mean the distance to the closest point in its cluster. If this is large, then the mean may be in between 2 clusters.
- Study covariance of data across all points in a cluster. It should be small if all points are similar.
- Compare distances between points in different clusters to distances between points in the same cluster. The within-cluster distances should be smaller.