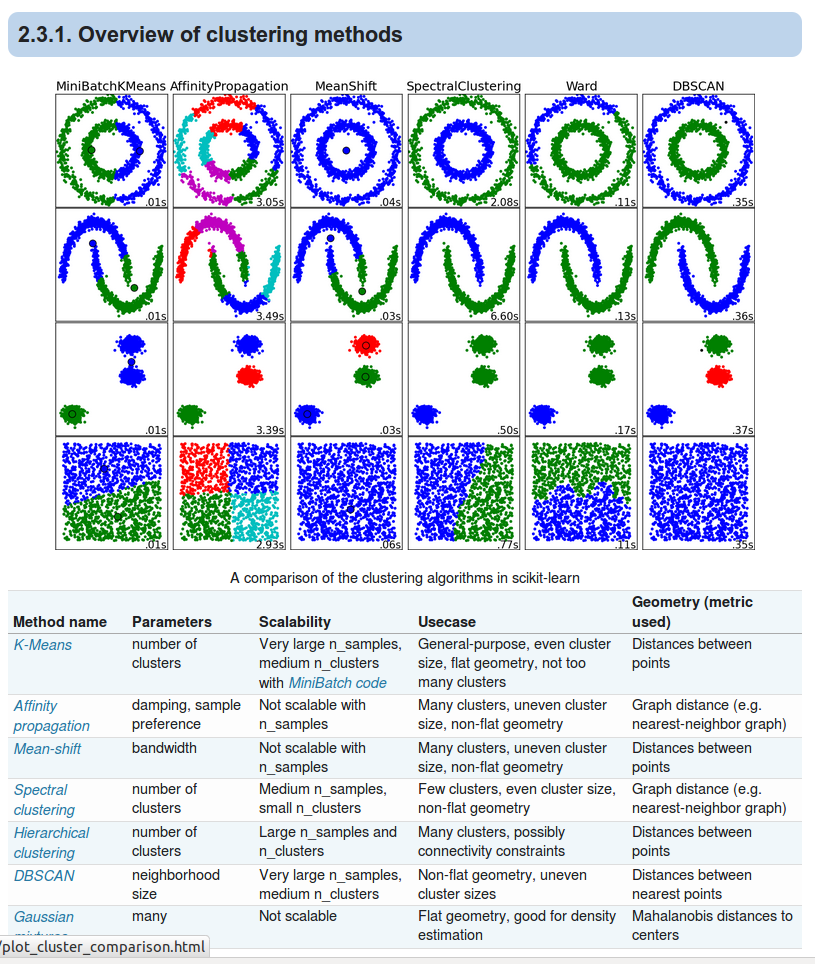
In [1]:
import matplotlib.pyplot as pl
import matplotlib.pyplot as pl
from numpy import *
def create_clustered_data(d,k,npercluster,r):
n = k*npercluster # total number points
# generate random points in unit square that are at least 2r apart
centers = [random.rand(d)]
while len(centers)<k:
trialcenter = random.rand(d)
farenough = True # optimistic!
for center in centers:
if linalg.norm(trialcenter-center,inf) < 2*r:
farenough = False
break
if farenough: centers.append(trialcenter)
centers = array(centers)
F = empty((n,d))
for i in range(k):
# create a cluster
start = i*npercluster
stop = (i+1)*npercluster
F[start:stop,:] = centers[i] + r*(2*random.rand(npercluster,d)-1)
return F,n
def plot_data_and_means(F,k,means,assignments):
colors = 'rgbmc' # red, green, blue, magenta, cyan
for i in range(k):
cluster = assignments==i
pl.plot(F[cluster,0],F[cluster,1],'.',color=colors[i],alpha=0.95);
pl.plot(means[i][0],means[i][1],'o',color=colors[i],markersize=50,alpha=0.1)
pl.plot(means[i][0],means[i][1],'.',color='k')
pl.xlim(-r,1+r); pl.ylim(-r,1+r)
return
def initialize_kmeans(F,k):
center = zeros(k,dtype=int)
center[0] = random.randint(n)
x = zeros((n,k))
for i in range(k-1):
x[:,i] = sum(square(F[center[i],:] - F),axis=1)
#plot(x[:,i])
center[i+1] = argmax(amin(x[:,0:(i+1)],axis=1))
means = F[center,:]
displacements = F[:,:,newaxis] - means.T # create 3D array (done after class)
sqdistances = (displacements**2).sum(axis=1) # Euclidean distance
assignments = argmin( sqdistances, axis=1 )
return means,assignments
def run_kmeans(F,k,max_iterations):
n=shape(F)[0]
oldassignments = k*ones(n,dtype=int)
count = 0
while(True):
count += 1
if count>max_iterations: break
# compute the cluster assignments
displacements = F[:,:,newaxis] - means.T # create 3D array (done after class)
sqdistances = (displacements**2).sum(axis=1)
assignments = argmin( sqdistances, axis=1 )
#print(assignments)
if all( assignments == oldassignments ): break
oldassignments[:] = assignments
# update the means as the centroids of the clusters
for i in range(k):
means[i] = F[assignments==i].mean(axis=0)
return means,assignments
So here's kmeans with nice initialization¶
In [2]:
d,k,npercluster,r,max_iterations = 2,5,25,0.05,100
F,n = create_clustered_data(d,k,npercluster,r)
means,assignments = initialize_kmeans(F,k)
means,assignments = run_kmeans(F,k,max_iterations)
plot_data_and_means(F,k,means,assignments)
Now for community detection. First compute distances between points¶
In [3]:
from pylab import *
displacements = F[:,:,newaxis] - F[:,:,newaxis].T
print(shape(displacements))
# displacements(i,0,k) gives difference between x_i and x_k
# displacements(i,1,k) gives difference between y_i and y_k
distances = (displacements**2).sum(axis=1)**.5 # Euclidean distance between all pairs of points
#print(shape(distances))
imshow(distances)
Out[3]:
Make network such that there are edges between nearby points¶
In [6]:
A = (distances<.05) - eye(n) # subtract identity matrix to remove self-edges
imshow(A) # here, yellow dots indicate and edge from node i to node j
edges = array((A).nonzero()).T
shape(edges)
Out[6]:
Use package networkX to analyze network data¶
In [8]:
from networkx import *
G = from_numpy_matrix(A)
nx.draw(G,node_size=10)
connected_components = sorted(nx.connected_components(G), key = len, reverse=True)
In [12]:
print(connected_components)
components_vector = zeros(n)
for i in range(len(connected_components)):
ids = [int(x) for x in list(connected_components[i])]
components_vector[ids] = i
components_vector
Out[12]:
In [13]:
nx.draw_networkx_nodes(G, pos=F, node_color=components_vector, node_size=10,alpha=0.8)
nx.draw_networkx_edges(G, pos=F, alpha=0.1)
shape(components_vector)
Out[13]:
Connected components work if the data is not noisy. If there are some edges between clusters (i.e., communities), you will need a better community detection algorithm.¶
download network file call football.gml¶
http://www.acsu.buffalo.edu/~danet/Sp18/MTH448/class23/class23_files/football.gml
In [16]:
H = nx.read_gml('football.gml') # graph markup language -- this is somebodies xml design
#nx.draw_networkx_nodes(H,pos=nx.spring_layout(H))
nx.draw(H,pos=nx.spring_layout(H))
In [17]:
# you must install with: pip install python-louvain
import community
partition = community.best_partition(H)# this finds the clusters using one algorithm
color_vec = list(partition.values())# we need a vector with the cluster ids to show clusters using color in a plot
labels2 = {a:a for a in list(nodes(H))} # to plot labels, you need a dictionary
nx.draw(H,pos=nx.spring_layout(H),node_color=color_vec,labels=labels2,font_size=10,alpha=.6 )