Support Vector Machines (SVM)¶
The Perceptron Learning Algorithm (PLA) identifies a plane $W$ that separates linearly separable data. The algorithm converges (i.e., stops) when such a plane is found. It does NOT seek to find the BEST plane.
To this end, we study support vector machines (SVMs). SVMs aim to find the maximum margin classifier as the solution of a quadratic programming problem. The approach involves 2 steps:
- Formulate the BEST plane as a convex optimizaiton problem
- Solve the convex optimization problem using quadratic programming
Below are the notes from class¶


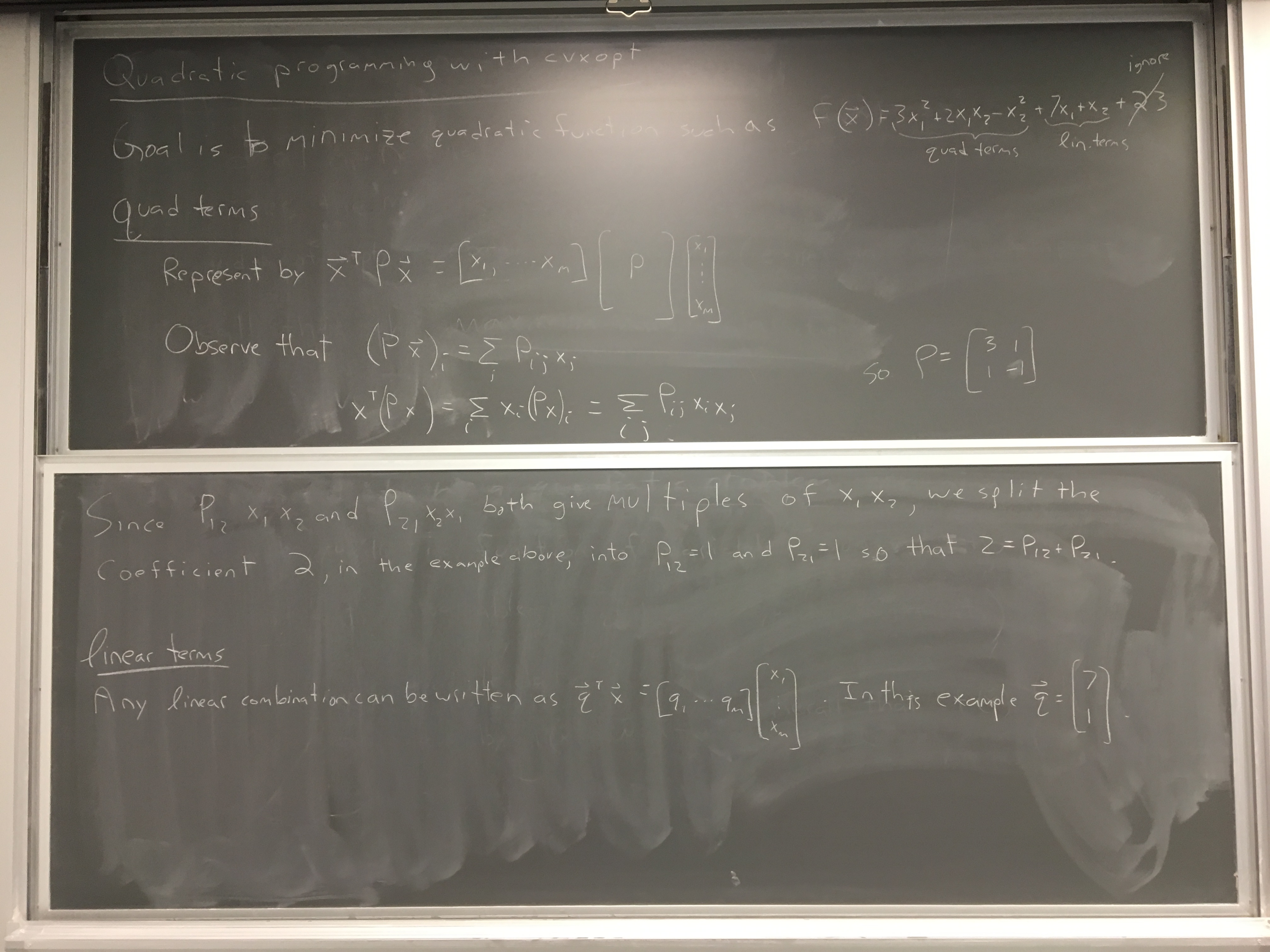
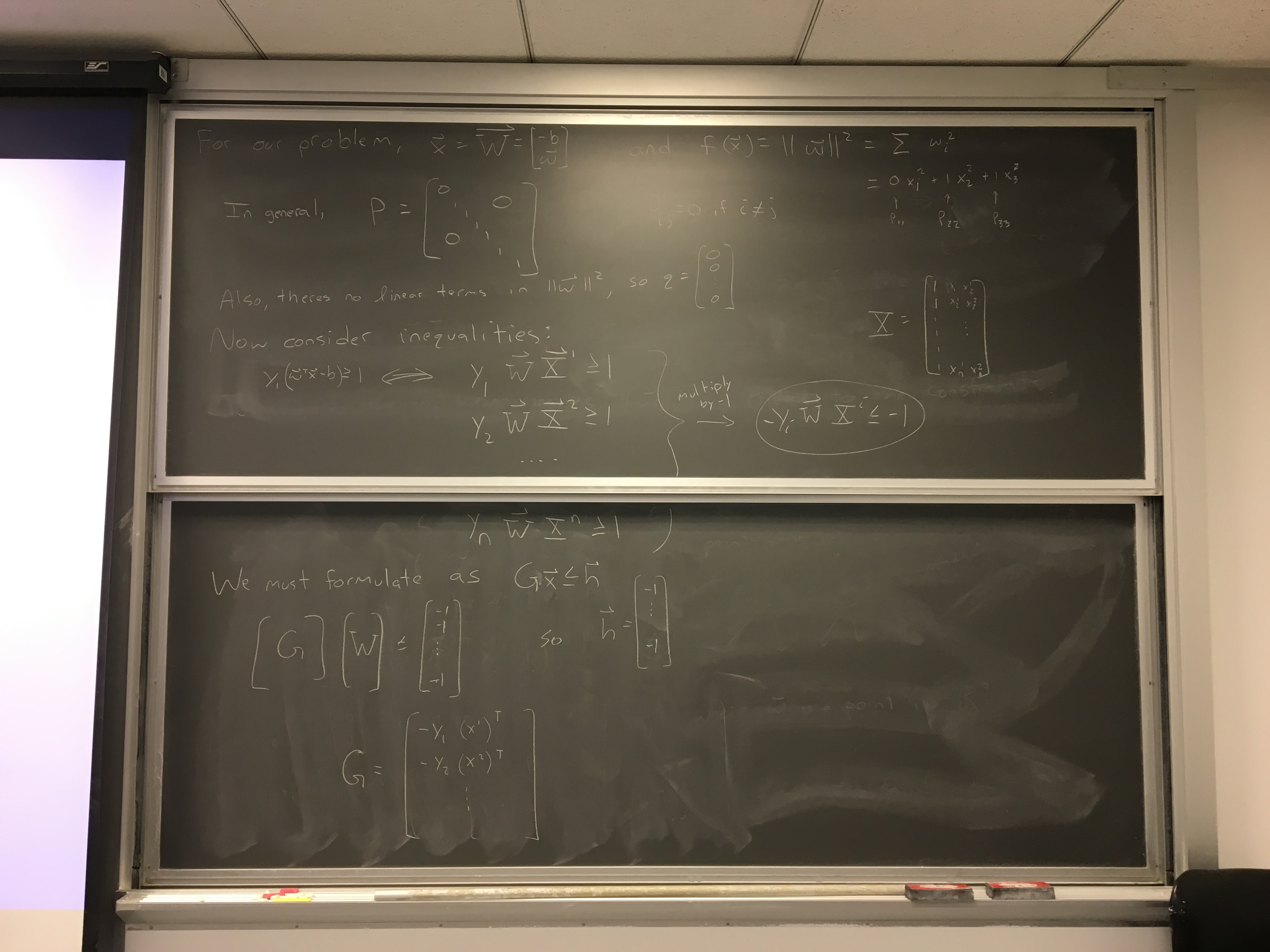
Let's first cook up some linearly separable data to study¶
def create_data(n,d):
x = random.rand(d,n) #randomly place points in 2D
X = empty((d+1,n))
X[0,:] = 1
X[1:,:] = x
y = sign(dot(W_true,X))
halfgap = 0.05
X[-1,y>0] += halfgap
X[-1,y<0] -= halfgap
return X,y
from numpy import *
d = 2 #2 dimensions
n = 50 #data points
W_true = array([-1,-2,3.]) # the true separating line (adding dot forces array to be a float array)
X,y = create_data(n,d);
#print(x)
print(X)
#print(y)
Create some functions to plot the data
def draw_points(X,y):
subplot(111,aspect=1)
xp = X[1:,y>0]
xm = X[1:,y<0]
plot(xp[0],xp[1],'rx')
plot(xm[0],xm[1],'bx');
def drawline(W,color='g',alpha=1.):
plot([0,1],[-W[0]/W[2],-(W[0]+W[1])/W[2]],color=color,alpha=alpha)
Now let's plot the data
%pylab inline
draw_points(X,y)
drawline(W_true,color='c',alpha=.5)
from cvxopt import matrix,solvers
P = eye(d+1)
P[0,0] = 0
q = zeros(d+1)
G = (-X*y).T
h = -ones(n)
P = matrix(P)
q = matrix(q)
G = matrix(G)
h = matrix(h)
Solve the problem¶
sol=solvers.qp(P,q,G,h)
type(sol)
sol.keys()
W = array(sol['x']).reshape(d+1)
print(W)
Plot the solution¶
draw_points(X,y)
drawline(W_true,color='c')
drawline(W,color='k')
Here is a second implementation that uses quadprog rather than cvxopt¶
import quadprog
def quadprog_solve_qp(P, q, G=None, h=None, A=None, b=None):
qp_G = .5 * (P + P.T) # make sure P is symmetric
qp_a = -q
if A is not None:
qp_C = -numpy.vstack([A, G]).T
qp_b = -numpy.hstack([b, h])
meq = A.shape[0]
else: # no equality constraint
qp_C = -G.T
qp_b = -h
meq = 0
return quadprog.solve_qp(qp_G, qp_a, qp_C, qp_b, meq)[0]
P = eye(d+1)
P[0,0] = .000000001
q = zeros(d+1)
G = (-X*y).T
#print(G)
h = -ones(n)
W2 = quadprog_solve_qp(P, q, G, h, A=None, b=None)
print(W2)
draw_points(X,y)
drawline(W_true,color='c')
drawline(W2,color='k')
SAME ANSWER¶
Exercise 1¶
Repeat homework 4 (cross validation) for the SVM and compare your results to the PLA.
Exercise 2¶
Consider 2-dimensional data with 4 class labels separated by 2 hyperplanes (visualize an x splitting the unit square into 4 domains). Modify the SVM algorithm to implement a decision tree that first separates according to one hyperplane and then according to the other.