I'm a Ph.D. candidate in Western New York, originally from Istanbul. I identify as an interdisciplinary computational mathematician (also he/him) and my study utilizes complex networks, dynamical systems, computational neuroscience and topological data analysis. In particular, I'm interested in both the theoretical model-driven analysis of nonlinear systems and the data-driven study of natural phenomenon. Subsequently, I foresee my PhD thesis will help me bridge neuro-related applications and math-related inspiration between domains.
I'm co-advised by Sarah Muldoon and Dane Taylor at University at Buffalo, State University of New York (SUNY). My work overlaps with their common research interests.
In my free time, I like exploring outdoors-- hopping around parks, backpacking, foraging mushrooms and trying to find a rock to boulder.

bengieru@buffalo.edu
Department of Mathematics
University at Buffalo, SUNY
106 Mathematics Building
Buffalo, NY, 14260-2900
USA
Research
Big data problems necessitate thinking of both imperfect and noisy nature of the real-world as well as complete and efficient nature of the theoretical study. In my work, I bridge two ends and think some data-related problems in the context of abstract simplicial complexes, hypergraphs and multilayer networks, of which we can compute particular properties, and try to develop the mathematical machinery in the interface of topological data analysis (TDA) and network-data analytics to tackle the problem.
So, as an inspired computational mathematician, my work falls under two complementary classes in which the former examines empirical data that is guided by the domain-expertise with neuroscience and the latter studies synthetic data generated by the neuron models and is guided by the bifurcation theory for dynamics:
For a detailed discussion of these topics, please reach out to me for my research statement.
Publications
I have given several contributed talks and presented posters in major conferences on complex networks, dynamical systems and neuroscience.
Talks
Posters
Teaching
One of the duties of my Ph.D. appointment is teaching/TAing the courses in the university. I have taught several key STEM courses in undergraduate math curriculum.
University at Buffalo, SUNY- Graduate Teaching Assistant, MTH141, College Calculus I, Fall'18
- Graduate Teaching Assistant, MTH142, College Calculus II, Spring'18/Spring'21
- Graduate Teaching Assistant, MTH241, College Calculus III, Fall'19/Fall'21/Spring'22
- Graduate Teaching Assistant, MTH309, Linear Algebra, Spring'20
- Graduate Teaching Assistant, MTH417, Survey of Multivariable Calculus, Spring'22
- Adjunct Instructor, MTH131, Mathematical Analysis For Management, Summer'19
- Adjunct Instructor, MTH241, College Calculus III, Summer'20
Code
I write modular, well-documented code in Python. Here are some example libraries I developed.
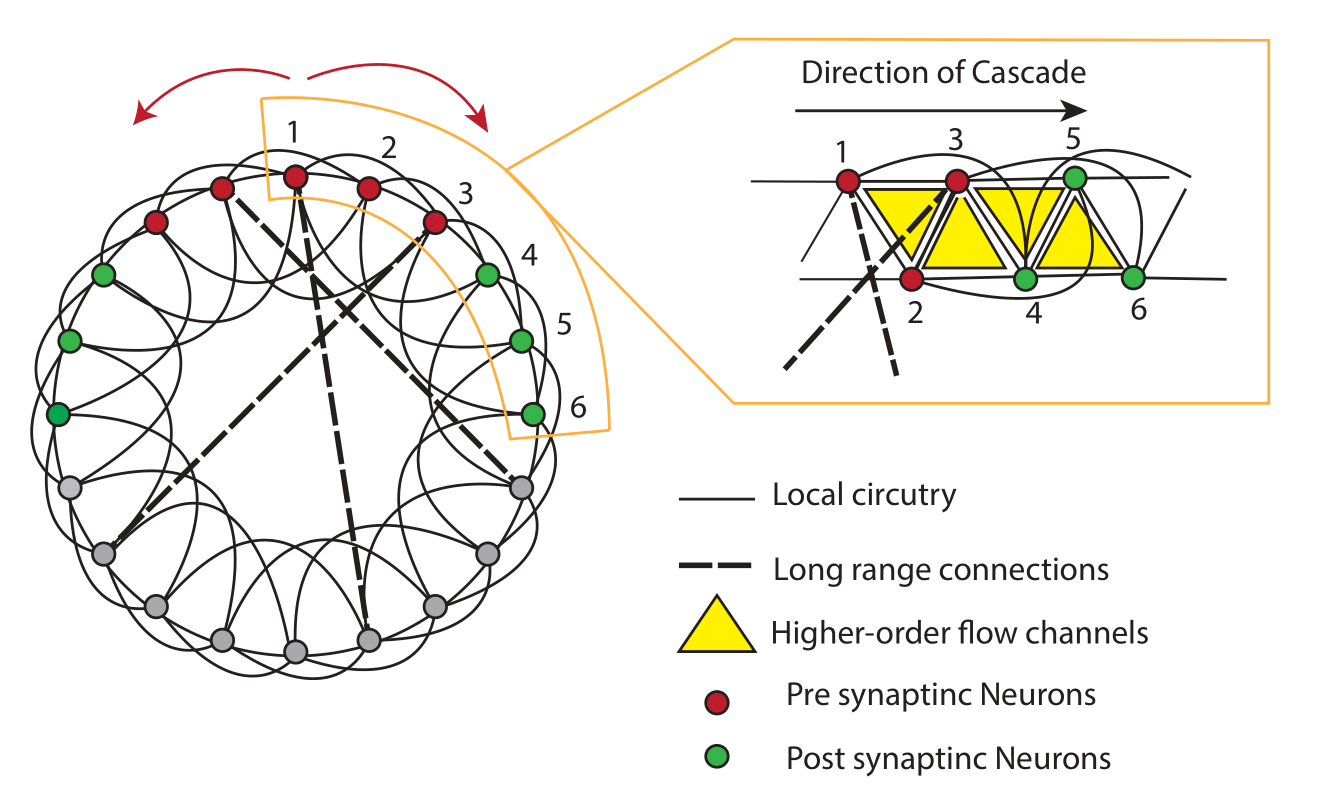
Neuronal Cascades- Neuronal Cascades is a python package to run an SI model on a custom-made geometric network and apply TDA (by computing persistent homology(PH)) on the distance matrices obtained by the contagion which recovers the manifold structure of the network.
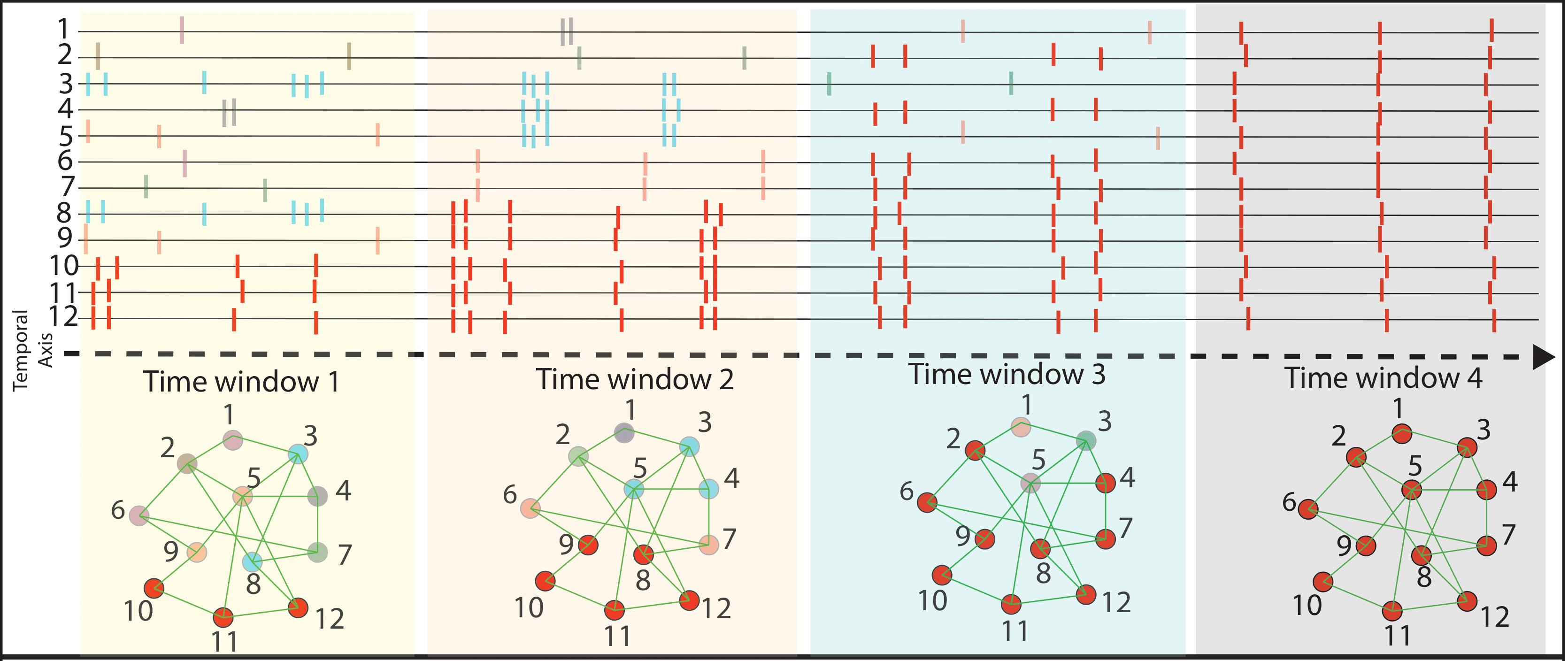
- Temporal Network Analysis is a python wrap-up for applying several dynamic community detection methods to time series data. Available options so far are Multilayer Modularity Maximization, Infomap, Tensor Factorization Approach and Dynamic Stochastic Block Model. Package also contains some helper functions for nice rendering of the communities across time.
- DONUTDA is another python package I coded for applying TDA to biomedical image segmentation. Algorithm takes grayscale images as input and builds cubical complexes. Applying PH yields either connected components or loops in the images. Accordingly, algorithm is suitable for localization/segmentation of different cell types, blob-like or donut-like. For the application oriented faculty and researchers, a graphical user interface is available.
